이번 글에서는 탄소나노튜브 구조 생성기를 만들면서 어떻게 수식화하고 일반화시키는지에 대해 소개합니다.
CNT Generator는 NxM의 CNT 구조를 바습 포맷에 맞게 만들어 주는 프로그램이다. CNT 어떻게 정의되는지와 타입을 알고, 그것에 따라 Unit cell을 정의하고 진공을 넣을 것이다. 말로 할 땐 쉽지만 실제로는 진짜로 머가리 깨져가며 계산했다.
탄소나노튜브(Carbon Nanotubes, CNT)를 정의하는 방법
탄소나노튜브(Carbon Nanotube, CNT)의 Roll-up Vector와 타입:
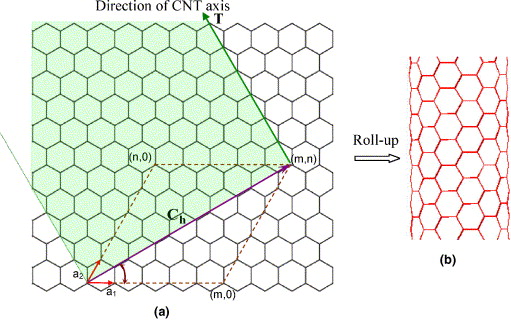
그림 출처: A.L. Kalamkarov et al., Analytical and numerical techniques to predict carbon nanotubes properties, International Journal of Solids and Structures (2006)
CNT는 그래핀 시트를 원통으로 말아놓은 구조이다.
a1 벡터, a2 벡터에서 각각 m배, n배 한 것을 보라색 와 같이 정의하는데, 이것을 Roll-up vector 혹은 Chiral vector라고도 부른다.
여기서 말아놓은 모양을 보고 크게 Armchair와 Zigzag 두 가지로 나눌 수 있다. Roll-up vector가 (m, 0)일 때가 zigzag, (m, m)이면 armchair가 된다. 인덱스의 두 숫자가 (m, n)과 같이 다르 다면 Chiral 타입이 된다.
그래서 나는 쓰는 사람이 편한 프로그램이 좋다고 생각하기 때문에, 입력 변수나 사용을 아주 쉽게 만들기로 했다. 그래서 사용자가 결정할 것은 암체어/지그재그 중에 무엇인지와 (m, 0), (m, m)에서 m이 끝이다.
CNT의 원주, 원자 위치를 계산하는 상세한 방법
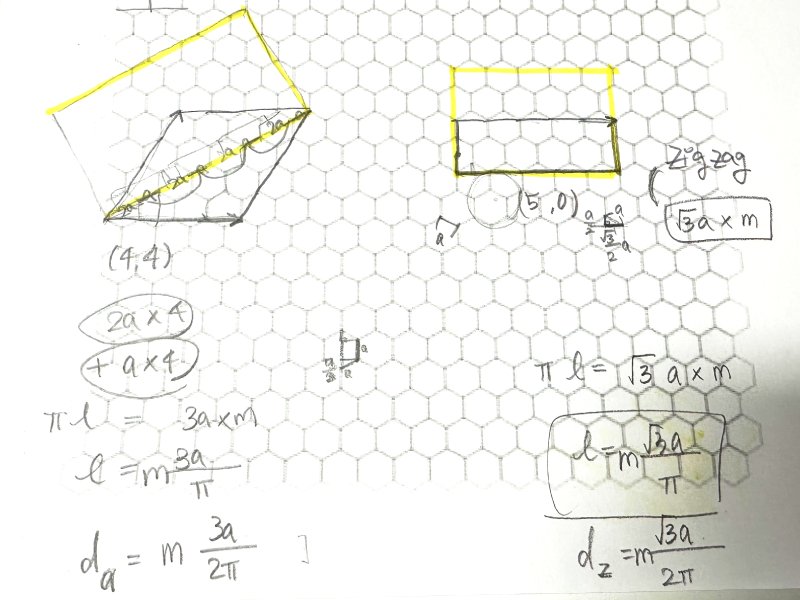
나한테는 지그재그가 좀 더 쉽게 느껴졌기 때문에 지그재그를 먼저 계산해봤다. 막상 풀고 나면 난이도에 큰 차이는 없는 것 같기도 하다. 어려운 수학적인 테크닉은 필요하진 않고.. 노가다가 필요하다. 이것을 계산하기 위해 알아야되는 지식은 두 가지이고, 추가적으로 필요한 능력은 하나다.
필요한 지식과 능력
- 60도, 30도, 90도 특수각 삼각형에서 각 변의 길이
- 원주 좌표계
- 중꺾마 (근성)
막상 해보고 나면 어렵진않다. 그러나 틀리면 고치고 다시 시작하는 건 좀 많다. 굉장히 많다.
지그재그 좌표와 원주 계산하기

먼저 A와 같은 유닛 셀을 찾았다. 유닛셀이 무한히 반복되는 고체에서는 translational symmetry가 있어 B와 같이 밑으로 민 것도 유닛 셀이 될 수 있다. A에서 B와 같이 유닛셀을 옮겨주면 (0, 0)에서 원자가 반복되어 계산이 조금 줄어드는 장점이 있다. 그리고 Cylindrical coordinate에서도 z의 높이가 모두 0으로 동일하다.
삼각형 변의 길이가 $$ 1:2:\sqrt(3) $$ 것을 이용하고, 원 위의 좌표인 사인, 코사인 계산을 열심히 해주면 계산할 수 있다.
정의, A.L. Kalamkarov et al.: https://doi.org/10.1016/j.i
레퍼런스 및 오픈 소스
- CNT의 정의, A.L. Kalamkarov et al.: https://doi.org/10.1016/j.ijsolstr.2006.02.009